maximos y minimos de una derivada

MAXIMOS Y MINIMOS  DE UNA DERIVADA

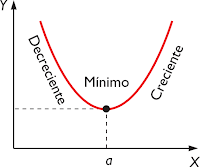En muchas ocasiones a través de los poderosos mecanismos de cálculo diferencial es posible encontrar respuesta a estos problemas, que de otro modo parecería imposible su solución. Entre los valores q puede tener una función (Y) puede haber uno que sea el más grande y otro que sea el más pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo absolutos. Si una función continua es ascendente en un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto crítico máximo relativo, aunque comúnmente se le llama solo máximo. Por el contrario, si una función continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos punto crítico mínimo relativo, o simplemente mínimo.                                                                                                           

METODOS PARA CALCULAR MAXIMOS Y MINIMOS DE UNA FUNCION

Para conocer las coordenadas de los puntos críticos máximos y mínimos relativos en una función, analizaremos dos mecanismos:

CRITERIO DE LA PRIMERA DERIVADA, UTILIZADO PARA UNA FUNCION CONTINUA Y SU PRIMERA DERIVADA TAMBIEN CONTINUA.

  obtener la primera derivada.

  igualar la primera derivada a cero y resolver la ecuación.

El valor o valores obtenidos para la variable, son donde pudiera haber máximos o mínimos en la función.

  se asignan valores próximos (menores y mayores respectivamente) a la variable independiente y se sustituyen en la derivada. Se observan los resultados; cuando estos pasan de positivos a negativos, se trata de un punto máximo; si pasa de negativo a positivo el punto crítico es mínimo.

Cuando existen dos o más resultados para la variable independiente, debe tener la precaución de utilizar valores cercanos a cada uno y a la vez distante de los demás, a fin de evitar errores al interpretar los resultados.

  sustituir en la función original (Y) el o los valores de la variable independiente (X) para los cuales hubo cambio de signo. Cada una de las parejas de datos así obtenidas, corresponde a las coordenadas de un punto crítico.

  CRITERIO DE LA SEGUNDA DERIVADA

Este método es más utilizado que el anterior, aunque no siempre es más sencillo. Se basa en que en un máximo relativo, la concavidad de una curva es hacia abajo y en consecuencia, su derivada será negativa; mientras que en un punto mínimo relativo, la concavidad es hacia arriba y la segunda derivada es positiva.

Este procedimiento consiste en:

  calcular la primera y segunda derivadas

  igualar la primera derivada a cero y resolver la ecuación.

  sustituir las raíces (el valor o valores de X) de la primera derivada en la segunda derivada.

Si el resultado es positivo, hay mínimo. Si la segunda derivada resulta negativa, hay un máximo.

Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.

  sustituir los valores de las raíces de la primera derivada en la función original, para conocer las coordenadas de los puntos máximo y mínimo.

Si f y f' son derivables en a, a es un mínimo relativo o local si se cumple:

1. f'(a) = 0          ;     2. f''(a) > 0

Cálculo de los máximos y mínimos relativos

f(x) = x³ − 3x + 2

1. Hallamos la derivada primera y calculamos sus raíces.                             f'(x) = 3x² − 3 = 0       ;          x = −1 x = 1.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:

f''(x) > 0 Tenemos un mínimo.

f''(x) < 0 Tenemos un máximo.

f''(x) = 6x

f’’ (−1) = −6 Máximo

f'' (1) = 6 Mínimo